Classification of Trapping SetsA list of possible candidates for trapping sets and corresponding subgraphs will be useful for analyzing Tanner graphs of any code. Such a list will make the trapping set identification process independent of the code. The problem of creating a list of possible candidates can be related to the coloring problems in graph theory. |
| Trapping Set (TS) | # TS | g=6 | g=8 | g=10 | g=12 | g=14 | g=16 |
|---|
| (3,3) | 1 | 1 | | | | | |
| (4,4) | 1 | | 1 | | | | |
| (4,2) | 1 | 1 | | | | | |
| (4,0) | 1 | 1 | | | | | |
| (5,5) | 1 | | | 1 | | | |
| (5,3) | 2 | 1 | 2 | | | | |
| (5,1) | 1 | 1 | | | | | |
| (6,6) | 1 | | | | 1 | | |
| (6,4) | 4 | 1, 2 | 3, 4 | | | | |
| (6,2) | 4 | 1, 2, 4 | 3 | | | | |
| (6,0) | 2 | 1 | 2 | | | | |
| (7,7) | 1 | | | | | 1 | |
| (7,5) | 6 | 1, 2, 5 | 3, 6 | 4 | | | |
| (7,3) | 10 | 1, 2, 5, 6, 7, 8, 9 | 3, 4, 10 | | | | |
| (7,1) | 4 | 2, 3, 4 | 1 | | | | |
| (8,8) | 1 | | | | | | 1 |
| (8,6) | 10 | 1, 2, 3, 5 | 4, 7, 9 | 6,10 | 8 | | |
| (8,4) | 25 | 1, 2, 3, 4, 5, 9, 10, 13, 14, 18, 19, 20, 21, 22, 23 | 6, 7, 8, 11, 15, 16, 17, 24, 25 | 12 | | | |
| (8,2) | 19 | 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 17 | 5, 15, 16, 18, 19 | | | | |
| (8,0) | 5 | 3, 4, 5 | 1, 2 | | | | |
|
Linear Space Characterization of Trapping Sets
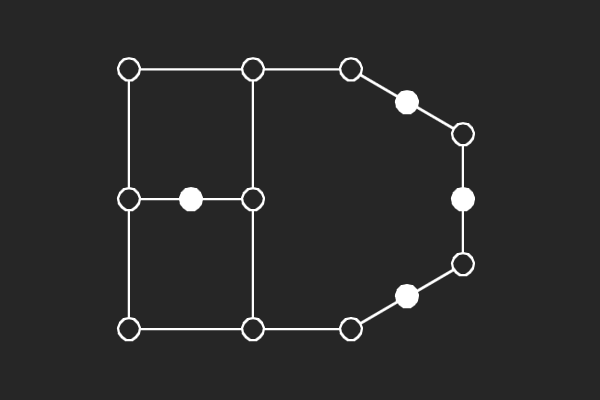
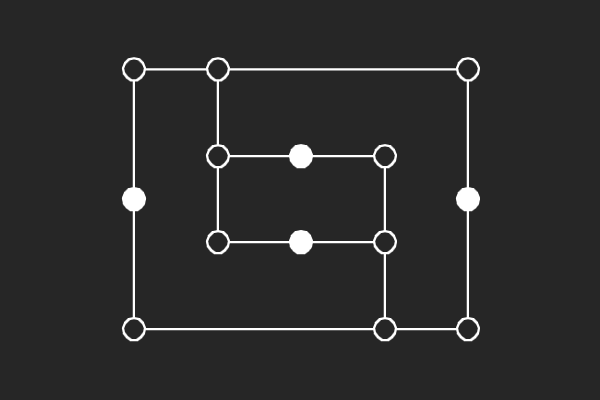
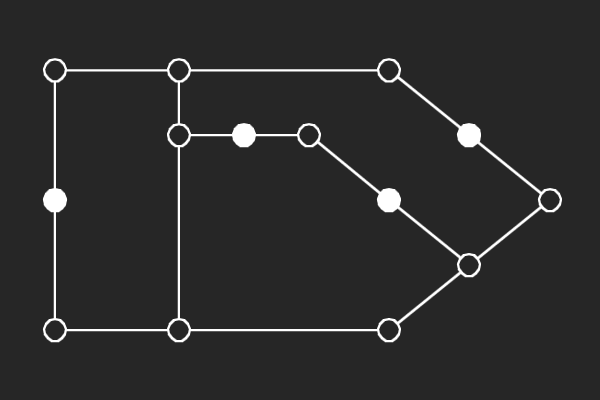
We choose an alternate graphical representation based on lines and points of finite linear spaces. In this representation, variable nodes correspond to lines and check nodes correspond to points. A point is solid if it has odd number of lines passing through it otherwise it is hollow. A subgraph corresponds to a possible trapping set if each line of the subgraph has more solid points than hollow points.
|
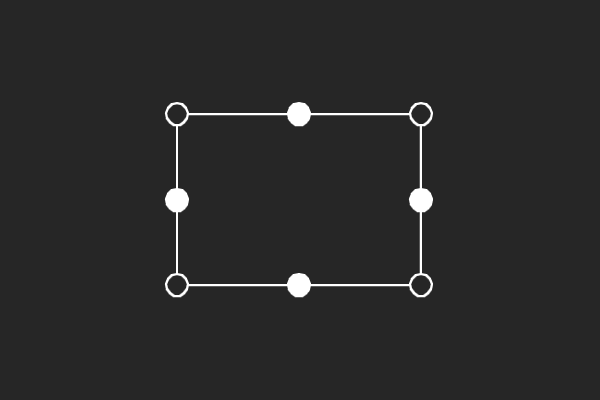 | 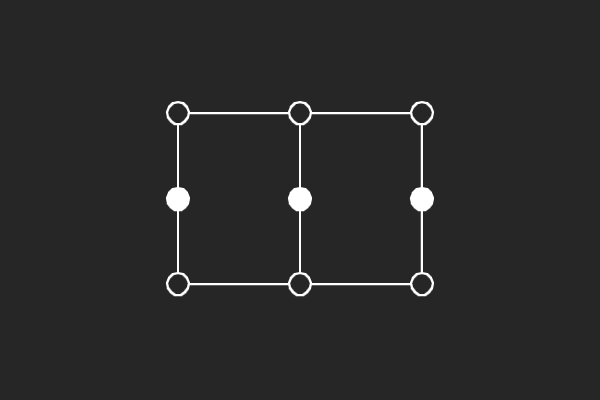 | 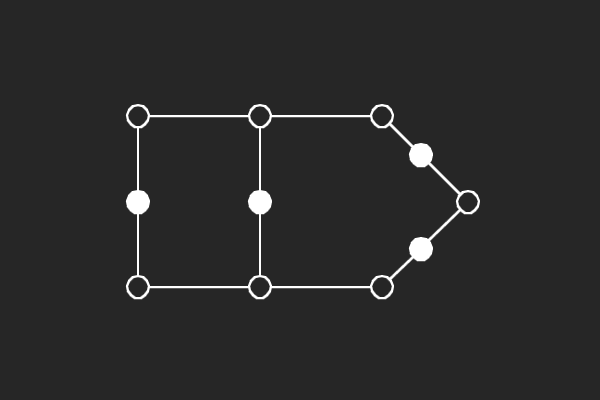 | 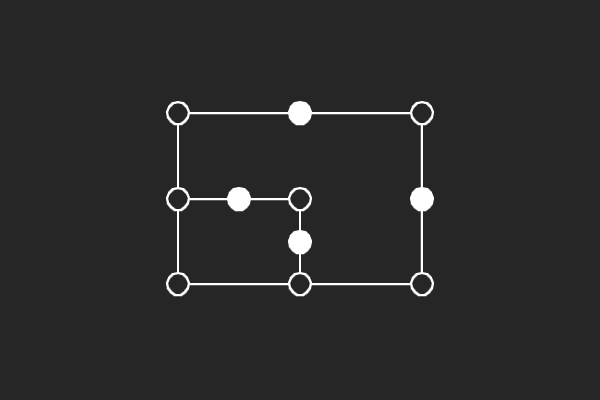 |
| (4,4){1} | (5,3){2} | (6,4){4} | (6,4){8} |
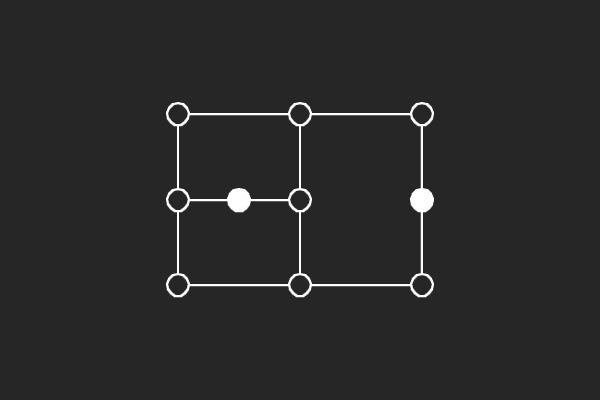 |  | 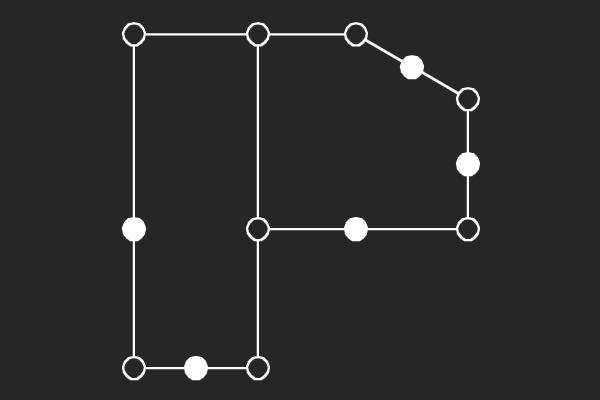 | 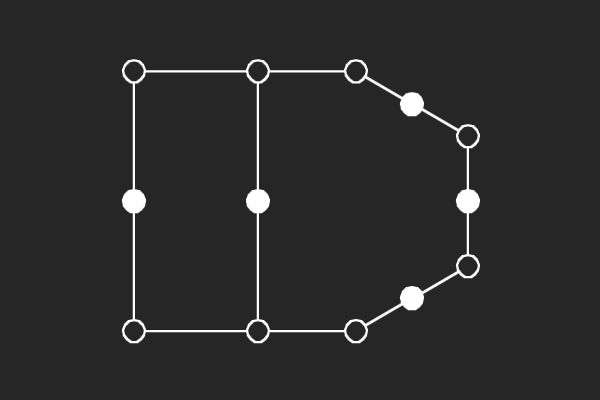 |
| (6,2){3} | (6,0){2} | (7,5){3} | (7,5){6} |
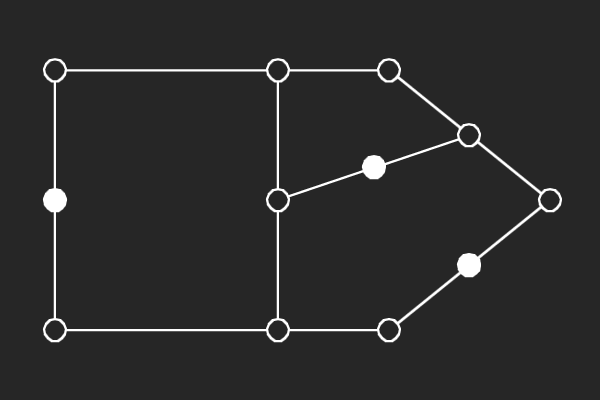 | 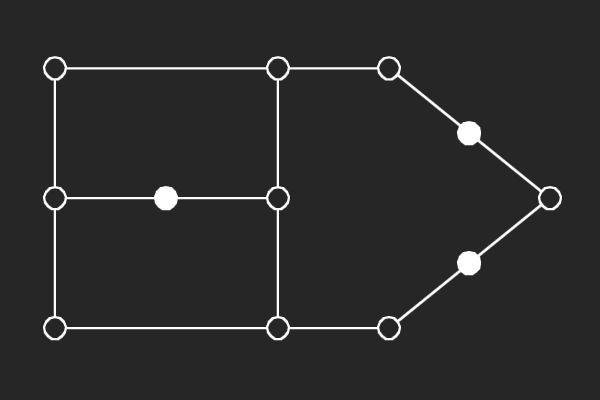 | 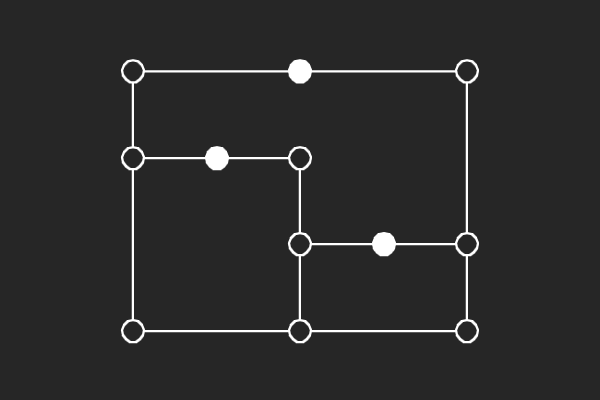 |  |
| (7,3){3} | (7,3){4} | (7,3){10} | (7,1){1} |
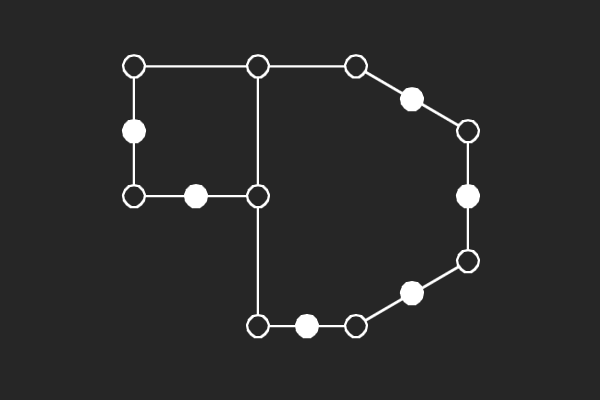 | 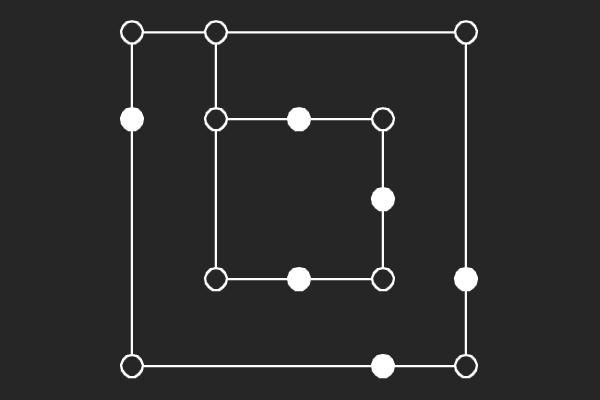 | 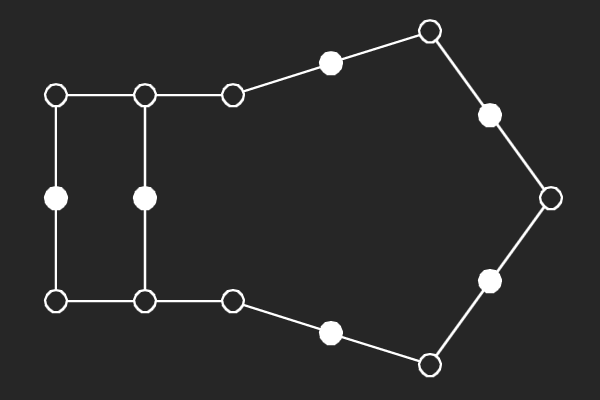 | 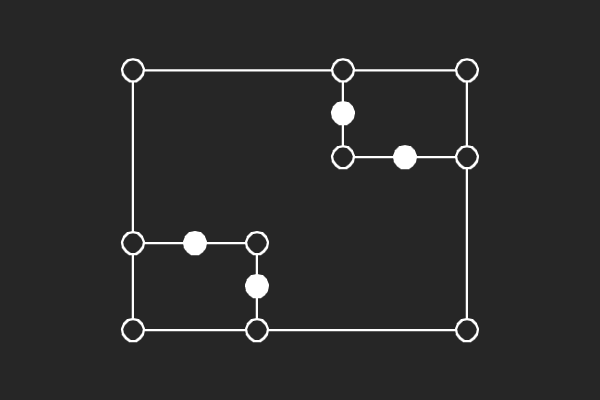 |
| (8,6){4} | (8,6){7} | (8,6){9} | (8,4){6} |
 |  | 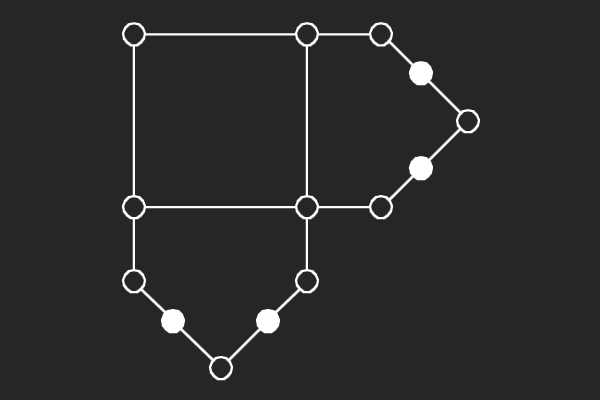 |  |
| (8,4){7} | (8,4){8} | (8,4){11} | (8,4){15} |
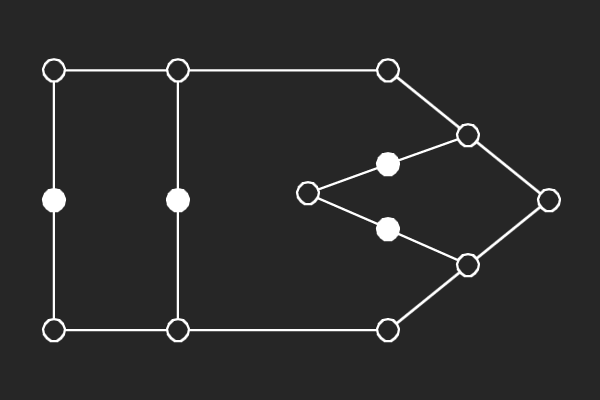 | 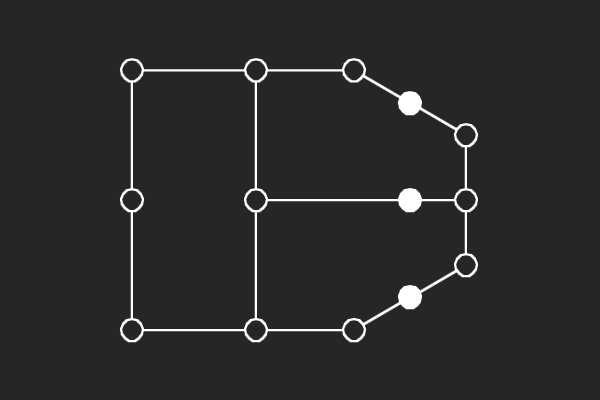 | 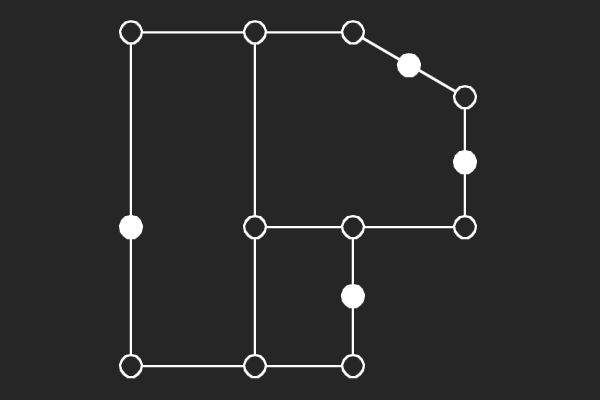 | 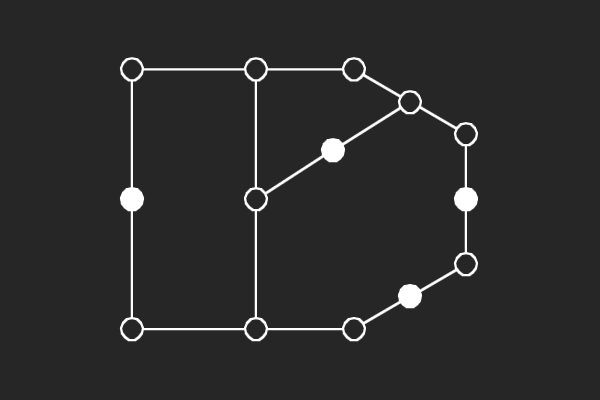 |
| (8,4){16} | (8,4){17} | (8,4){24} | (8,4){25} |
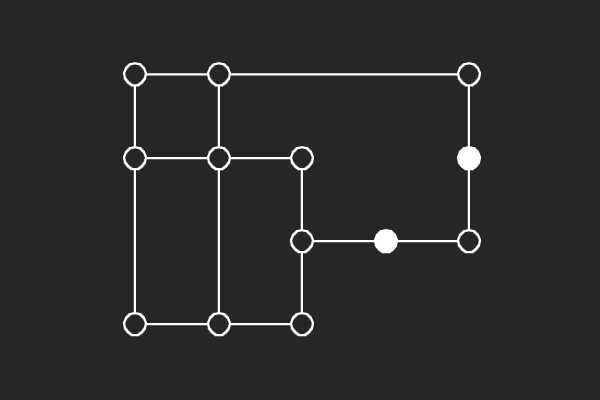 | 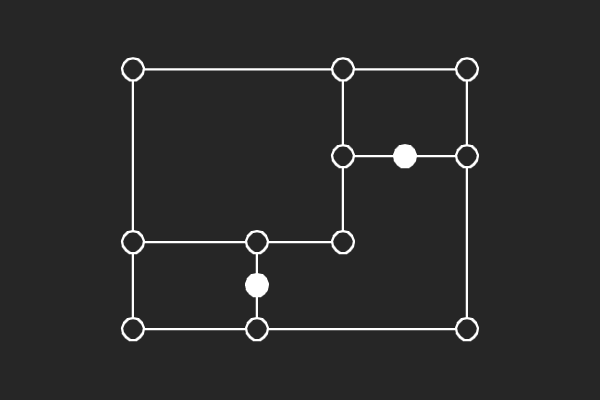 | 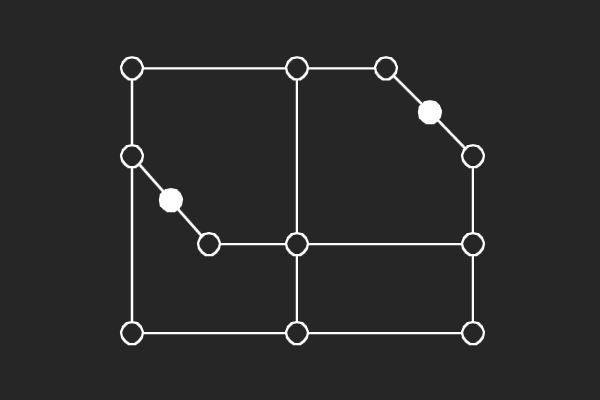 | 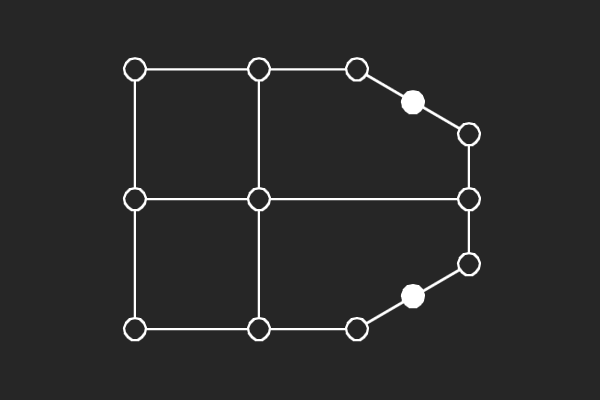 |
| (8,2){5} | (8,2){15} | (8,2){16} | (8,2){8} |
 | 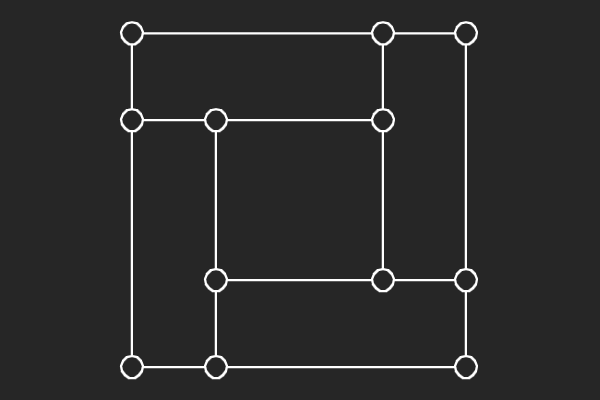 | 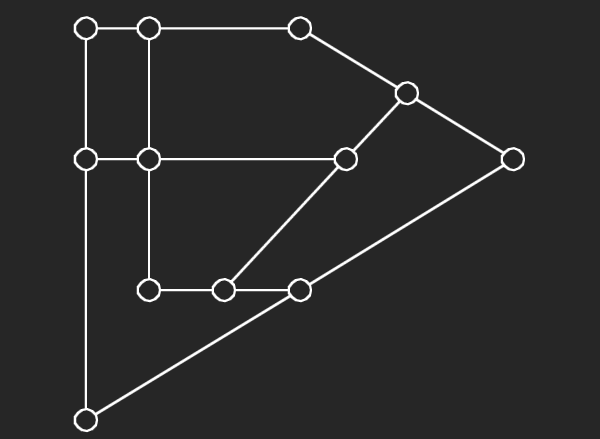 |
| (8,2){19} | (8,0){1} | (8,0){2} |
| Trapping Set | Parents | Children |
|---|
| (4,4){1} | | All remaining trapping sets |
| (5,3){2} | (4,4){1} | (6,2){3}, (6,0){2}, (7,3){4}, (7,1){1}, (8,4){7}, (8,2){16}, (8,2){18} |
| (6,4){3} | (4,4){1} | (7,3){3}, (7,3){10}, (8,4){6}, (8,4){16}, (8,4){25}, (8,2){5}, (8,2){15}, (8,2){19},
(8,0){1}, (8,0){2} |
| (6,4){4} | (4,4){1} | (7,3){3}, (7,3){4}, (7,1){1}, (8,4){11}, (8,4){15}, (8,4){17}, (8,2){5} |
| (6,2){3} | (4,4){1}, (5,3){2} | (7,1){1}, (8,2){16} |
| (6,0){2} | (4,4){1}, (5,3){2} | |
| (7,5){3} | (4,4){1} | (8,4){15}, (8,4){17}, (8,4){24}, (8,4){25}, (8,2){19} |
| (7,5){6} | (4,4){1} | (8,4){7}, (8,4){8}, (8,4){16}, (8,4){24}, (8,2){15}, (8,2){16}, (8,2){18} |
| (7,3){3} | (4,4){1}, (6,4){3}, (6,4){4} | (8,2){5}, (8,2){19}, (8,0){2} |
| (7,3){4} | (4,4){1}, (5,3){2}, (6,4){4} | (8,2){18} |
| (7,3){10} | (4,4){1}, (6,4){3} | (8,2){15}, (8,0){1} |
| (7,1){1} | (4,4){1}, (5,3){2}, (6,4){4}, (6,2){3} | |
| (8,6){4} | (4,4){1} | |
| (8,6){7} | (4,4){1} | |
| (8,6){9} | (4,4){1} | |
| (8,4){6} | (4,4){1}, (6,4){3} | |
| (8,4){7} | (4,4){1}, (5,3){2}, (7,5){6} | |
| (8,4){8} | (4,4){1}, (7,5){6} | |
| (8,4){11} | (4,4){1}, (6,4){4} | |
| (8,4){15} | (4,4){1}, (6,4){4}, (7,5){3} | |
| (8,4){16} | (4,4){1}, (6,4){3}, (7,5){6} | |
| (8,4){17} | (4,4){1}, (6,4){4}, (7,5){3} | |
| (8,4){24} | (4,4){1}, (7,5){3}, (7,5){6} | |
| (8,4){25} | (4,4){1}, (6,4){3}, (7,5){3} | |
| (8,2){5} | (4,4){1}, (6,4){3}, (6,4){4}, (7,3){3} | |
| (8,2){15} | (4,4){1}, (6,4){3}, (7,5){6}, (7,3){10} | |
| (8,2){16} | (4,4){1}, (5,3){2}, (6,2){3}, (7,5){6} | |
| (8,2){18} | (4,4){1}, (5,3){2}, (6,4){4}, (7,5){6}, (7,3){4} | |
| (8,2){19} | (4,4){1}, (6,4){3}, (6,4){4}, (7,5){3}, (7,3){3} | |
| (8,0){1} | (4,4){1}, (6,4){3}, (7,3){10} | |
| (8,0){2} | (4,4){1}, (6,4){3}, (6,4){4}, (7,3){3} | |
|






























